Alle vorgeschlagenen Pläne waren dem Weihnachtsmann zu asymmetrisch.
Er ist sich nicht sicher, warum er dich überhaupt gefragt hatte, und hat nun selber einen Park designt, der zwar mehr als die minimale Anzahl Teleporter erfordert, aber dafür (seiner Meinung nach) deutlich eleganter aussieht.
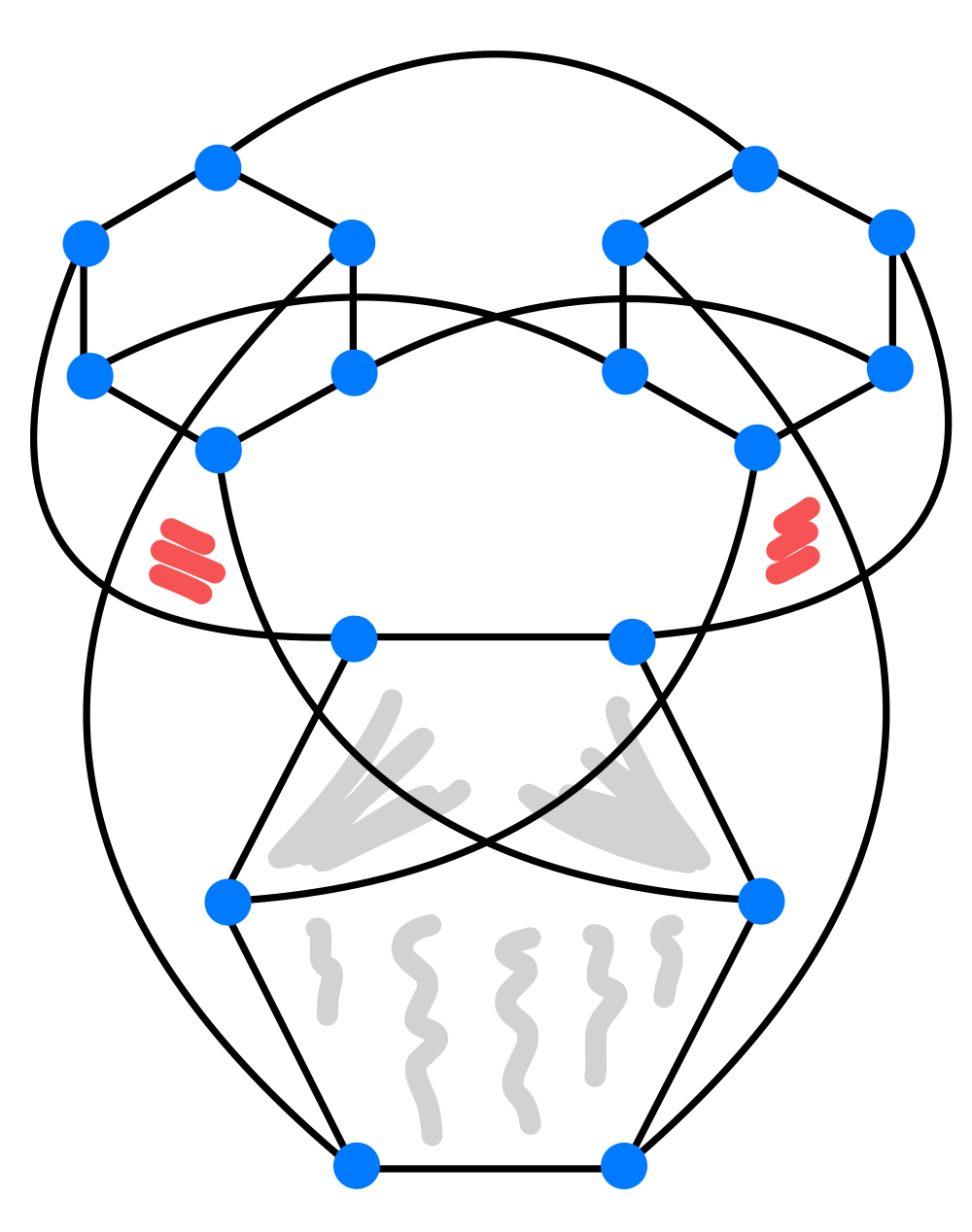
Moment mal... bei genauerer Betrachtung sieht das ja aus wie...
Na, jetzt ist immerhin klar, warum dem Weihnachtsmann maximales Sparen doch nicht mehr so wichtig war!
Nach einer anstrengenden Geschenkeproduktionsphase, bei der du heute aushelfen durftest, laden dich einige der Wichtel auf eine Schneeballschlacht ein. Frederik erklärt dir seine Strategie:
„In der Vorbereitungsphase von Schneeballschlachten lege ich meist ein Schneeballlager an, während Christel häufig eher Verstecke baut und Rudolf Zeit in das Finden einer strategisch günstigen Position investiert. Da die Kugeln so gut ineinander gelegt werden können, ergeben sich in dieser Zeit bei mir manchmal sechseckähnliche Formen. Dann geht die Schneeballschlacht los und ich kann mein Lager leider nur selten in dieser schönen Form beibehalten...“
Eigentlich wolltest du genau zuhören, welche Regeln bei dieser Schneeballschlacht gelten sollen, aber automatisch gehst du im Kopf durch, wie diese Sechseckkonfigurationen aussehen...

Kleine solche Sechsecke bestehen aus 1, 7 oder 19 Schneebällen. Komisch, \(1=1^3\), \(1+7=8=2^3\), \(1+7+19=27=3^3\) sind ja die ersten Kubikzahlen! Gilt für jedes natürliche \(n\), dass die Summe der \(n\) kleinsten Kardinalitäten von Seckseck-Schneeball-Sammlungen stets \(n^3\) entspricht? Hoffentlich kommst du schnell auf die Lösung, sonst wirst du in der kommenden Schneeballschlacht nicht gut dastehen....

