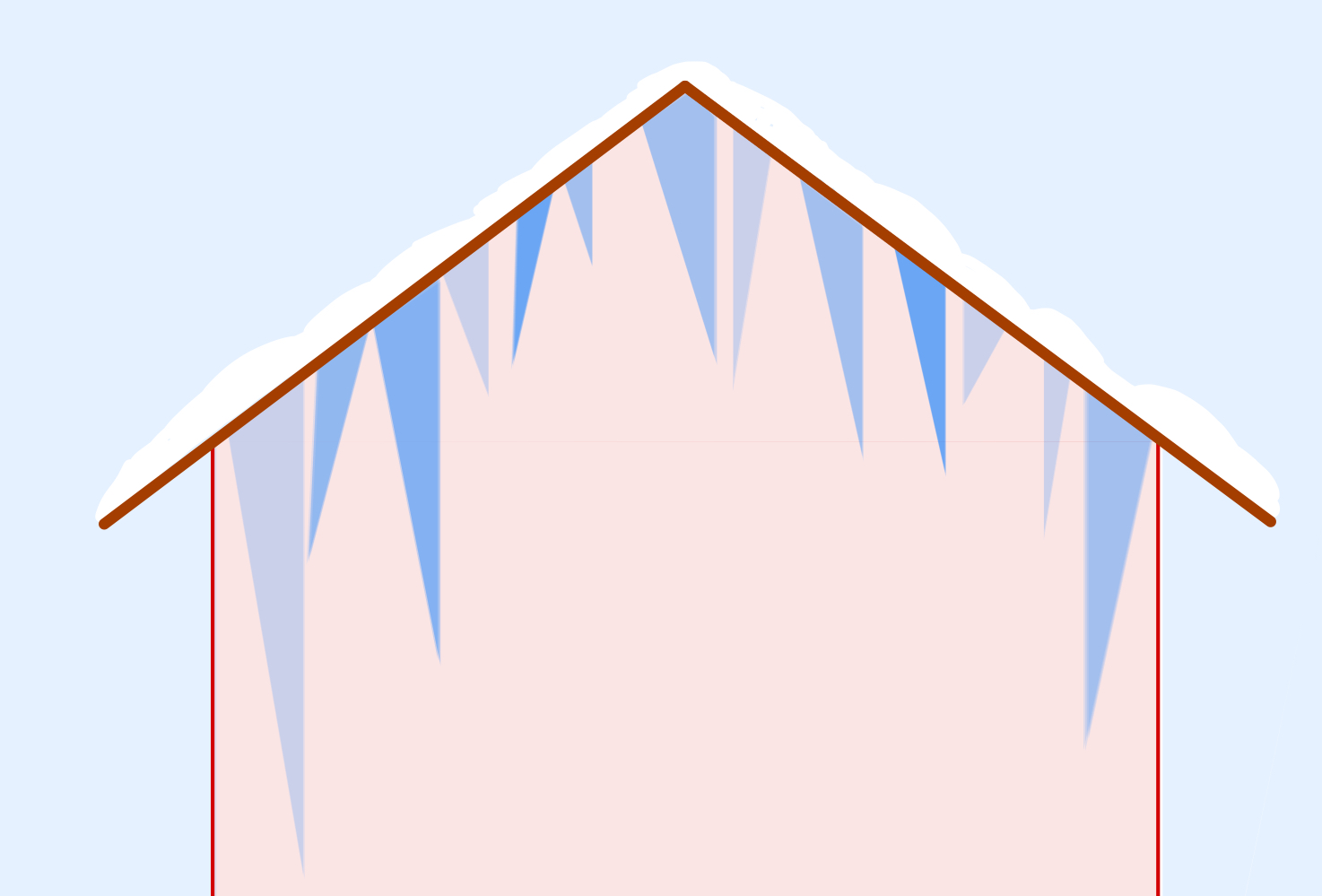
Eine Spielsituation, in der schon einige Eiszapfen abgebrochen wurden.

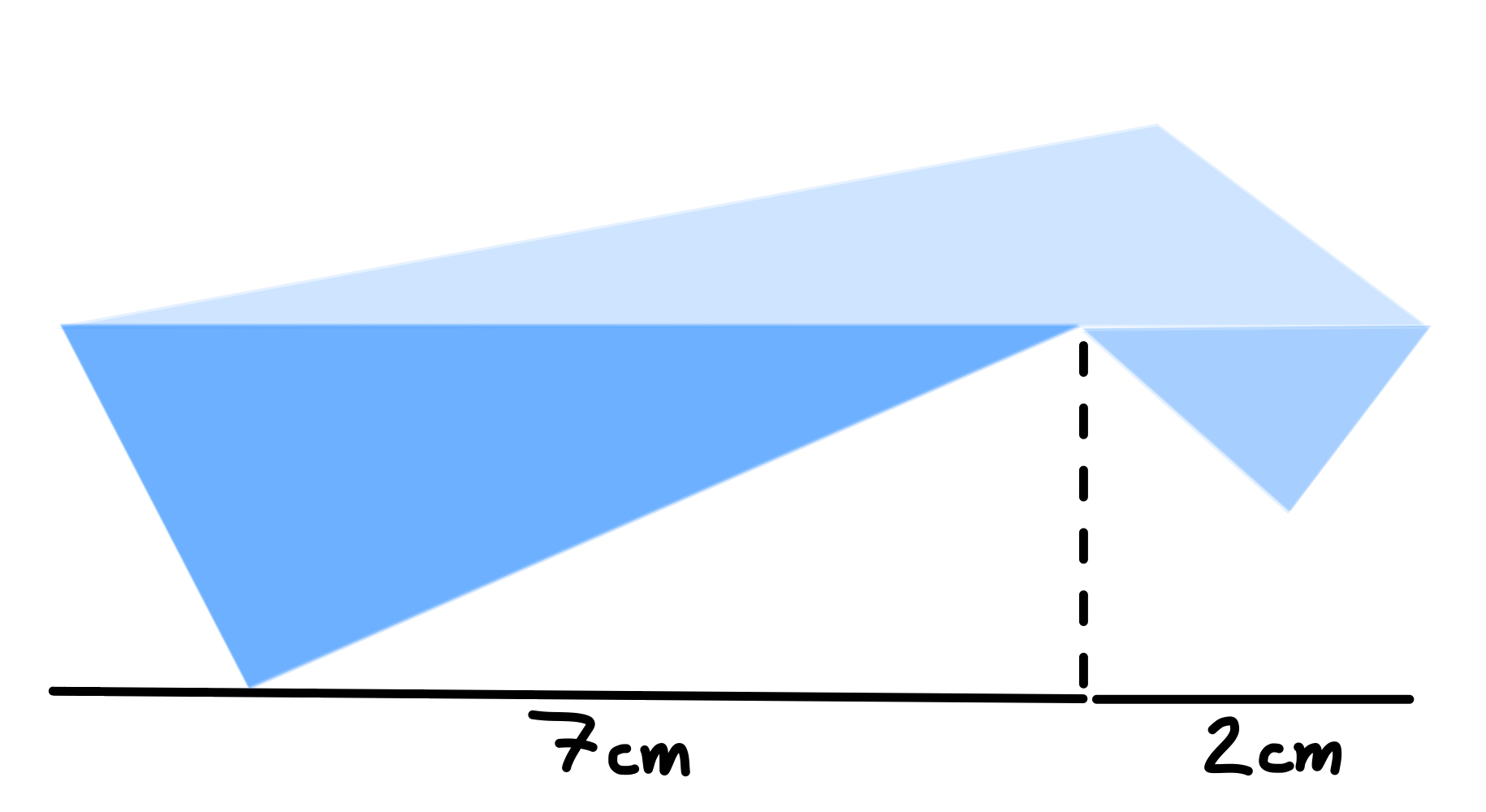
Links ist ein valides Dreieck, rechts lässt sich kein Dreieck legen, da aus den Zapfen mit den Längen 2 cm, 7 cm und 9 cm nur eine Linie entstehen kann.
Die schnellste und schönste Lösung ist von Niemandem.
Der Weihnachtsmann ist zufrieden mit deinem Entwurf für den Geschenkeraum. Die Menge an Glassteinen liegt sogar noch in der Schlittenhalle bereit, sodass der Schlitten schon bald bereit für seine erste große Fahrt sein wird. Heute besuchst du daher mal wieder die Wichtel.
In den letzten Tagen haben sich viele gefährlich große Eiszapfen gebildet. Zur Sicherheit wollen die Wichtel diese von den Häusern abbrechen, aber sie haben sich daraus ein Spiel gemacht und wollen es heute mit dir spielen. Frederik möchte der erste sein, der es gegen dich spielen darf, und erklärt dir die Regeln:
„Wir starten mit den 25 Eiszapfen der natürlichen Längen 1 cm bis 25 cm, die dort an diesem einen Haus hängen. Die Länge wird immer an der längsten Strecke von der Spitze des Eiszapfens bis zur baldigen Bruchkante gemessen und alle abgebrochenen Zapfen sehen aus einer bestimmten Richtung von der Seite betrachtet wie Dreiecke aus, und zwar aus der Richtung, von der aus man gut diese längste Strecke messen kann. Jeder von uns bricht abwechselnd einen Zapfen ab. Wenn nur noch drei Eiszapfen am Dachüberstand hängen, schauen wir, ob sie sich zu einem Dreieck legen lassen, wobei die drei gemessenen Seiten das Dreick bilden müssen. Falls das funktioniert, gewinnt der erste Spieler, falls es nicht geht, der zweite. Bitte, bitte, darf ich anfangen?!“
Du fragst dich, ob du Frederik diesen Wunsch gewähren solltest, wenn du gewinnen möchtest. Oder ist vielleicht auch egal, wer anfängt?

Eine Spielsituation, in der schon einige Eiszapfen abgebrochen wurden.


Links ist ein valides Dreieck, rechts lässt sich kein Dreieck legen, da aus den Zapfen mit den Längen 2 cm, 7 cm und 9 cm nur eine Linie entstehen kann.
Eine schnelle Lösung gibt an, ob der erste, der zweite oder keiner von beiden Spielern eine Gewinnstrategie hat. Eine schöne Lösung gibt diese an und beweist sie.