Das Sekretariat konnte nicht zählen und hat nun Bild und Bildunterschrift korrigiert.
In deinem etwas schickeren Zimmer hast du es dir nun gemütlich gemacht. Tagsüber begleitest du Anja zu ihrer Geschenkewerkstatt.
Einige Weihnachtswichtel haben sich dort das Ziel gesetzt, in einigen ihrer Pausenräume Lichterketten anzubringen. Christel möchte dir die genauen Pläne erzählen, da es noch zwei offene Fragen gab, aber sie hat ein wichtiges Detail vergessen. Sie erinnert sich noch an Folgendes:
„Wir wollen lauter verschiedene Lichterketten basteln und haben dafür bereits viele noch identisch aussehende Lichterketten gesammelt. Jede der Lichterketten hat 2n Lämpchen, für ein natürliches n, und für mehr Abwechslung wollen wir um je n der Lämpchen einen gelben Bascettastern basteln, um die anderen n Lämpchen kleine Papierbäumchen. Dann leuchtet jede Kette in zwei Farben! Damit es nicht langweilig wird, soll keines der Stern-Baum-Muster doppelt vorkommen. Da wir ganz exakt basteln können, sehen natürlich jeweils alle Sterne und alle Bäume gleich aus. Die Lämpchen der Lichterkette sind wie an einer Schnur aufgereiht und da in allen Pausenräumen die Steckdosen gleich verteilt sind, wissen wir schon, dass der Stecker immer links sein sollte. Wir würden gerne in jeden Pausenraum, von dem aus Wichtel mitwirken, n+1 Lichterketten hängen.
Ich hab aber komplett vergessen, was denn jetzt n war... Oh weh.“
Trotz einiger Grübelei kommt sie einfach nicht auf die Zahl. Dann fährt sie nach einem Schulterzucken fort:
„Also, wir wollten fragen, ob es möglich ist, die fertigen Lichterketten unter diesen Bedingungen gleichmäßig auf die Pausenräume aufzuteilen. Außerdem finden wir keine schöne Form, wie viele Pausenraum-Wichtelgruppen denn mitwirken müssen, damit alles aufgeht. Ach, wüsste ich doch, was n ist...“
Kannst du Christel helfen, auch wenn du n nicht kennst?
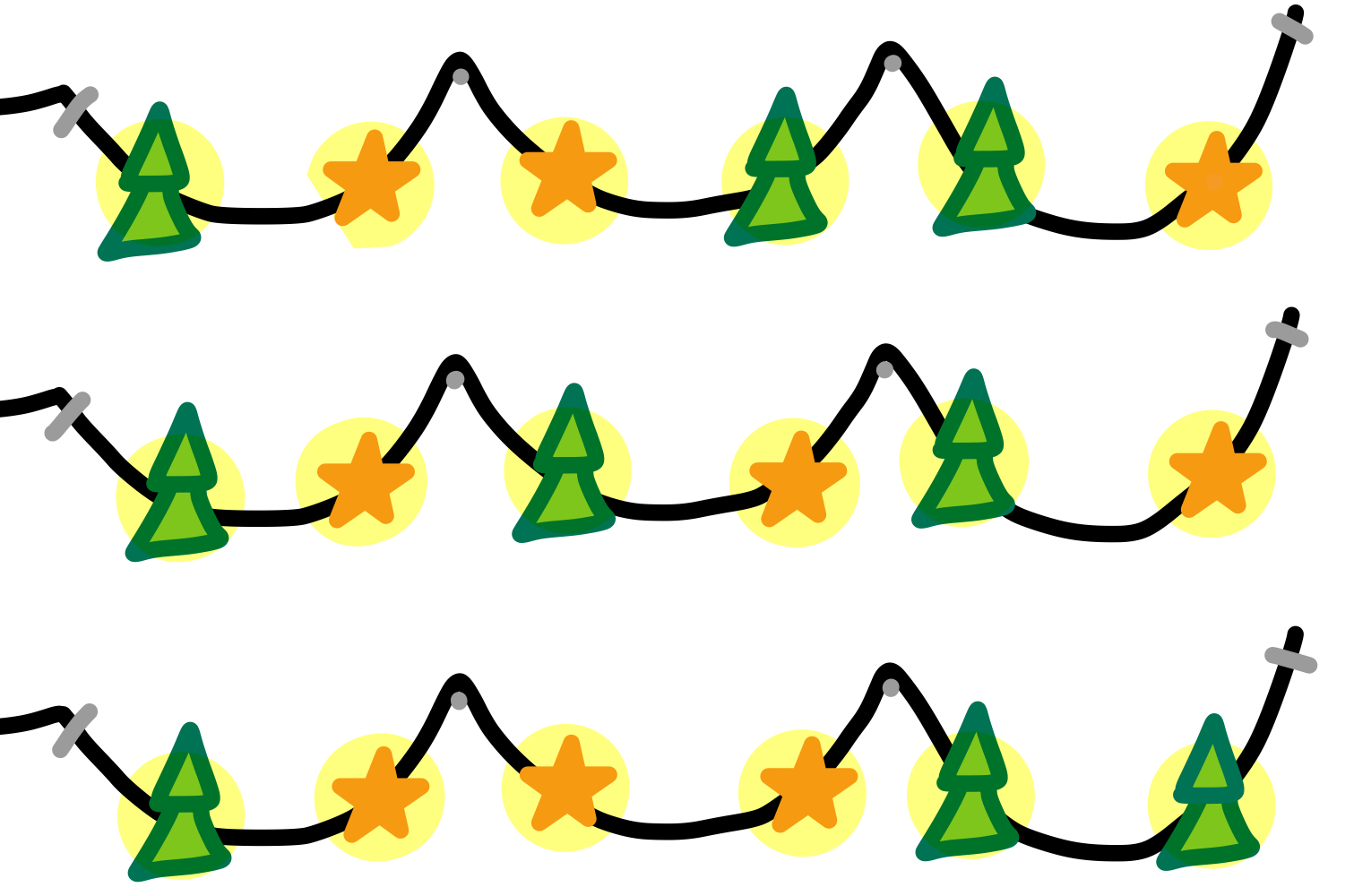
Drei als verschieden zu zählende Lichterketten, falls n=3. Die Kabelei am linken Bildrand wird aus ästhetischen Gründen nicht abgebildet. Natürlich ist dies nur eine schematische Darstellung. Das weihnachtliche Sekretariat bemüht sich zwar um eine akkurate Aufzeichnung aller Geschehnisse, aber Bascettasterne zeichnen ist dann doch zu viel verlangt!
Eine schnelle Lösung liefert die Informationen, die Christel helfen: Ist das Unterfangen unabhängig von n möglich, so ist zu nennen (dies kann eine "unschöne Form" annehmen), wie viele Pausenraum-Wichtelgruppen mitbasteln können. Ist das Unterfangen nicht für alle n möglich, so ist eine (hinreichende und notwendige) Bedingung für n anzugeben, wann der Plan aufgeht.
Eine schöne Lösung enthält im ersten Fall zusätzlich eine Begründung für Christel, warum die Lichterketten gleichmäßig auf die Pausenräume aufteilbar sind. Im zweiten Fall enthält eine Lösung einen Nachweis für die Bedingung.