Lampenaufhängung

Die schnellste Lösung stammt von Wichtel42, die schönste vom Kalkülaus.

Der neue Schlitten ist bestellt und nun kann es endlich mit den Vorbereitungen für Weihnachten losgehen. Auch die Wichtel machen sich bereit und wollen zuerst das Weihnachtsdorf auf Vordermann bringen. Schließlich kommt erst richtig Stimmung in die Runde, wenn die Umgebung passt, denn Wichtel arbeiten nicht einfach so, es muss schon eine weihnachtliche Atmosphäre bestehen!

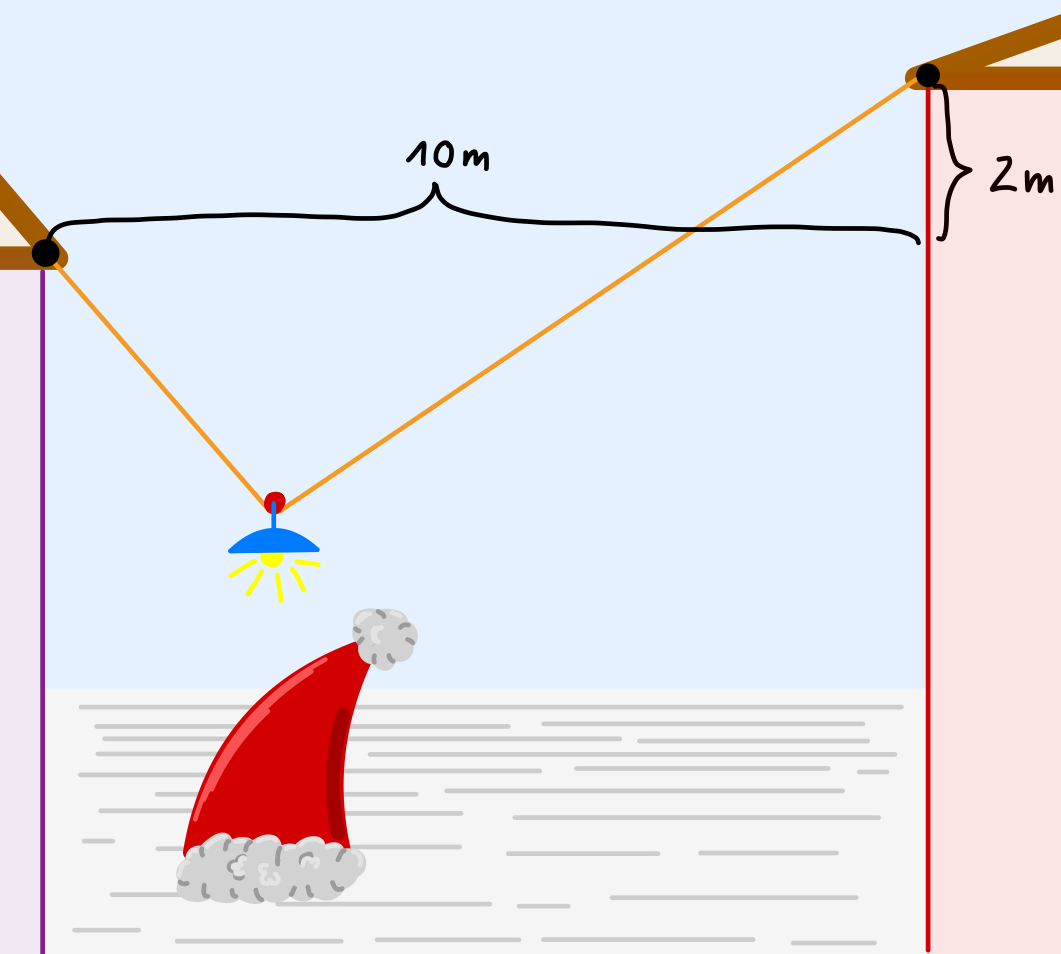
Unter anderem wollen sie dafür zwischen zwei Häusern eine Lampe aufhängen, die die Lieblingsstatue des Weihnachtsmannes beleuchten soll: eine menschengroße Zipfelmütze aus Ton. Die Wichtel wollen ein Zauberband, welches 13 Meter lang ist, zwischen die Häuser hängen, auf dem eine Lampe auf einer Rolle nach links und rechts rollen kann, bis sie über der Statue zur Ruhe kommen soll.

Allerdings haben die Aufhängepunkte an den Häusern einen Höhenunterschied von zwei Metern und einen horizontalen Abstand von zehn Metern (aus Betrachterperspektive gibt es keine Tiefendifferenz). Daher wird die Lampe vermutlich nicht mittig stehen bleiben.

Das Zauberband hat immerhin die Eigenschaft, dass es nichts wiegt und stets straff gespannt ist, da die Lampe genügend wiegt, um es herunterzuziehen. Außerdem besteht keine Reibung zwischen Rolle und Band. Damit die Wichtel die Statue optimal beleuchten können, wollen sie nun wissen, wie weit (horizontal) vom linken Haus entfernt die Rolle, an der die Lampe hängt, zur Ruhe kommt. Dann können sie die Statue mittig darunterstellen. Du nimmst dir einen Stift und ein Blatt Papier und beginnst mit einer Skizze...

Eine schnelle Lösung nennt den gesuchten horizontalen Abstand exakt. Eine schöne Lösung beschreibt auch den Lösungsweg. Die Nutzung technischer Hilfsmittel ist dabei nur schön, wenn ausschließlich Lösungen von Gleichungen in einer (!) Variablen damit bestimmt werden.

Lösung

Die Lösung des Kalkülaus ist schöner als die des weihnachtlichen Sekretariats und kommt ganz ohne den Einsatz von Technik aus. Mit Einverständnis des Kalkülaus wird das Vorgehen hier wiedergegeben.

Die Lampe kommt aufgrund der Schwerkraft dort zur Ruhe, wo sie am niedrigsten hängt. Stellt man sich eine horizontale Gerade \(g\) durch die Lampenrolle vor und spiegelt den linken Aufhängungspunkt, genannt \(A\), an dieser, so hängt die Lampe am Punkt \(C\) dann am tiefsten, wenn die \(A\)-Spiegelung \(A'\), \(C\) und der rechte Aufhängungspunkt \(B\) auf einer Geraden liegen (an dieser Stelle wird an Wichtelintuition appelliert).

Der Abstand \(x\) zwischen dem Schnittpunkt von \(g\) mit der rechten Hauswand und \(B\) beträgt \(\sqrt{(13m)^2-(10m)^2} = \sqrt{69}m\), der Abstand zwischen \(A\) und \(A'\) beträgt \((x-2)m=(\sqrt{69}-2)m\). Der vertikale Abstand zwischen \(A'\) und \(C\) beträgt dementsprechend \(\frac{\sqrt{69}-2}{2}m\).

Mit dem Strahlensatz erhalten wir nun eine Gleichung für den gesuchten Abstand \(d\), denn es muss \[\frac{10m}{x} = \frac{d}{a/2},\text{ also}\] \[d = \frac{a}{2x} \cdot 10m = \frac{\sqrt{69}-2}{2\sqrt{69}} \cdot 10m = (5 - \frac{10}{\sqrt{69}})m \approx 3,79614m\].

Man verzeihe mir bitte den kursiven Meter, MathJax und ich haben ein schwieriges Verhältnis.