Weihnachsstiefel

„Dann ist ja jetzt fast alles fertig! Ach, ohne dich wäre das alles wirklich nichts geworden. Ich hätte nicht rechtzeitig mit den Vorbereitungen angefangen, hier wäre wesentlich weniger schön dekoriert worden und einige der Wichtel haben mir auch schon erzählt, was sie alles von dir gelernt haben. Daher möchte ich dich einladen, mich auf der heutigen Geschenke-Tour zu begleiten, die ja schließlich mit deiner Hilfe geplant wurde.“ Du bist ganz gerührt von den Worten des Weihnachtsmannes. „Natürlich möchte ich mitfliegen!“, antwortest du freudestrahlend, und er fährt sogleich fort:

„Auf meinem feinen Snow Rider fliegen wir ziemlich schnell, daher sollte man Schutzkleidung tragen. Ich habe Hose, Jacke und Mütze doppelt, aber der Schaft des rechten Ersatzstiefels ist beschädigt. In seinem derzeitigen Zustand würde der Stiefel vom Flugwind vermutlich zerstört werden und du könntest auskühlen. Aber bestimmt kann der Stiefelmacher-Schneemann noch schnell einen neuen anfertigen, wenn wir ihm sagen, was er herstellen soll. An so einen Flugstiefel stellt man ganz besondere Anforderungen, ich habe nur leider vergessen, welche Realisierungen der Anforderungen gut funktionieren.“

Gespannt spitzt du die Ohren. Das klingt ja so, als würde gleich ein besonders schwieriges Rätsel folgen!

„Der optimale Schaft \(S\) wird während der Stiefelproduktion als gerade stehender hohler Zylinder ohne Grund- und Deckfläche interpretiert. Der Schaft soll 30 cm hoch sein und einen Durchmesser von 20 cm haben, da die Hose in ihn hineingesteckt werden muss. Weihnachtsstiefel bestehen aus einem Material namens TriKraft, das keine Biegungen zulässt, daher wird der Schaft aus einer Vielzahl von Dreiecken konstruiert. Immerhin sichert dies die Windbeständigkeit! Das verwendete Material hat keine relevante Dicke, da es speziell für diese Weihnachtskleidung entwickelt wurde und ich so viel laufen muss, dass meine Stiefel möglichst leicht sein sollten. Für die Konstruktion orientiert man sich wie folgt am angestrebten \(S\):

Der Schaft \(S\) wird in \(m\) gleich große Ringe zerlegt, indem man \(S\) mit horizontal liegenden Ebenen schneidet. Jeder Ring hat also eine Höhe von \(\frac{30}{m}\) cm und wird durch einen oberen und einen unteren Kreis begrenzt. Jeder der Ringe wird nun mit gleich großen Dreiecken gefüllt. Dies geschieht, indem die begrenzenden Kreise in \(n\) kongruente Kreisbögen unterteilt werden. Die Unterteilungspunkte jedes zweiten Kreises liegen exakt vertikal übereinander, aber die Unterteilungspunkte zwischen zwei benachbarten Kreisen sind genau um eine halbe Kreisbogenlänge verschoben. Verbindet man die Unterteilungspunkte zwischen zwei benachbarten Kreisen nun auf naheliegende Weise, so ergeben sich pro Ring lauter kongruente gleichschenklige Dreiecke.“

Deinen angestrengten Blick bemerkend, kramt der Weihnachtsmann aus einer Tasche einen zerknitterten Zettel hervor. „Komm, ich zeig's dir:

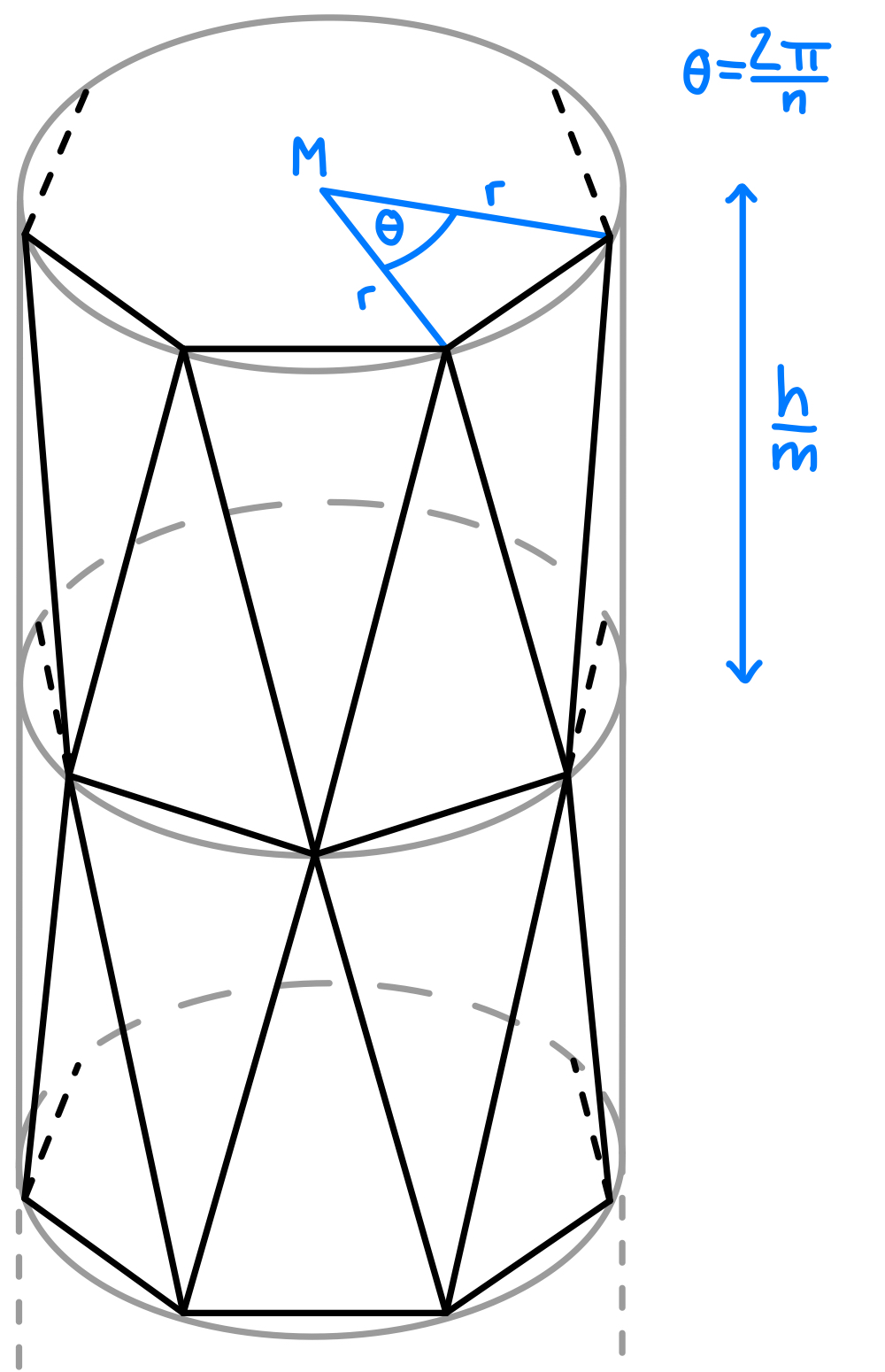
Dies ist ein angedeuteter herstellbarer Stiefelschaft, hier wäre \(n=7\), ich habe nur nicht alle Linien eingezeichnet. \(h\) meint die Höhe des gesamten Stiefels, \(r\) den Radius. Ich hatte früher bereits allgemeiner über optimale Stiefelkonstruktionen nachgedacht, da die früheren Stiefelprototypen bei einigen Wahlen von \(m\) und \(n\) merkwürdig kratzig wurden.

Der weihnachtliche Stiefelmacher probiert natürlich, eine möglichst feine Unterteilung zu wählen, also große \(m\) und \(n\). Ich erinnere mich noch, dass aber je nach Unterteilungsverhältnis sehr unterschiedliche Mengen TriKraft gebraucht werden. Da es nur schwer zu beschaffen ist, sollten wir ein Verhältnis wählen, das zu wenig Verbrauch führt. Verschnitt wird von so einem Profi aber natürlich vollständig vermieden! Nur welches Verhältnis eignet sich dafür?“

Sollte der Stiefelmacher-Schneemann für große \(n\) eher eine Stiefelverfeinerung mit \((m,n)=(n,n)\) oder mit \((m,n) = (2 \sqrt{3} \frac{30}{\pi^2 \cdot 20} n^2, n)\) wählen?

(Über die nicht-Natürlichkeit von \(m\) im zweiten Fall ist hier bitte hinwegzusehen. Nach der Abstraktion der Situation für natürliche \(m\) ergibt sich hoffentlich, wie damit umzugehen ist. Wem damit nicht behaglich ist, der denke sich für genügend große \(n\) ein natürliches \(m\) möglichst dicht an \(2 \sqrt{3} \frac{30}{\pi^2 \cdot 20} n^2\))

Eine schnelle Lösung gibt an, welches der beiden Stiefelschaft-Unterteilungsverhältnis für große \(n\) weniger TriKraft verbraucht und wie viel Material in den zwei Verhältnissen bei starker Verfeinerung ungefähr (also im Grenzwert) benötigt werden würde. Eine schöne Lösung beweist die Korrektheit der schnellen Lösung. Einheitenloses Rechnen ist in dieser Aufgabe in Ordnung. Für diese Aufgabe gibt es Tipps, die orientierungslose Wichtel (und auch andere) gerne nutzen können.